2.3. Binary Representation of Data

Here we briefly consider the format used to store data variables in memory and in registers.

2.3.1. Integer Variables

Unsigned variables that generally fall into the category of integers (char, short, int, long) are stored in straight binary format, beginning with all zeros for zero up to all ones for the largest number that can be represented by the data type.

The signed variables that generally fall into the category of integers (char, short, int, long) are stored in 2’s – compliment format. This ensures that the binary digits represent a continuous number line from the most negative number to the largest positive number with zero being represented with all zero bits. The most significant bit is considered the sign bit. The sign bit is one for negative numbers and zero for positive numbers.

Any two binary numbers can thus be added together in a straight forward manner to get the correct answer. If there is a carry bit beyond what the data type can represent, it is discarded.

   1        0x0001
+(-1)     + 0xffff
------    ---------
   0        0x0000

To change the sign of any number, invert all the bits and add 1.

2 = 0x0002 = 000...010  ==> 111...101
                           +        1
                           -----------
                            111...110 = 0xfffe = -2

2.3.2. Conversions of Integer Variables

It is often necessary to convert a smaller data type to a larger type. For this, there are either special instructions (Intel x86), or a sequence of a couple simple instructions (Sun SPARC) to promote a variable to a larger data type.

If the variable is unsigned, then extra zeros are just filled into the most significant bits (movezx move - zero extending, for Intel x86).

For signed variables, then the sign bit needs to be extended to fill the most significant bits (movesx move - sign extending, for Intel x86).

0x6fa1  ==> 0x00006fa1   (sign extend a positive number)

0xfffe  ==> 0xfffffffe   (sign extend a negative number)
0x9002  ==> 0xffff9002   (sign extend a negative number)

2.3.3. Floating Point Data

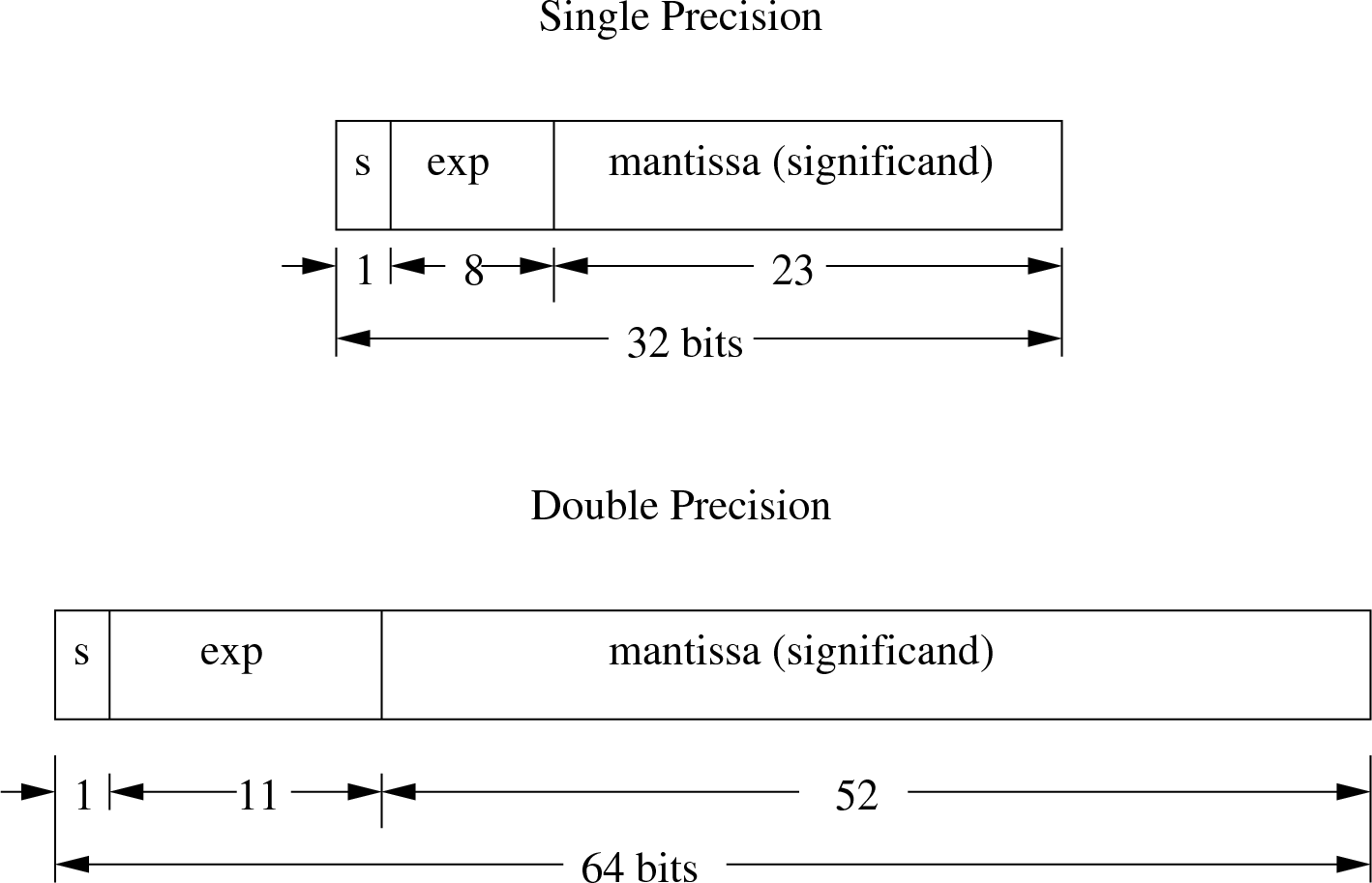
Floating point variables have been represented in many different ways inside computers of the past. But there is now a well adhered to standard for the representation of floating point variables. The standard is known as the IEEE Floating Point Standard (FPS). Like scientific notation, FPS represents numbers with multiple parts: a sign bit, one part specifying the mantissa and a part representing the exponent. The mantissa is represented as a signed magnitude integer (i.e., not 2’s Compliment), where the value is normalized. The exponent is represented as an unsigned integer which is biased to accommodate negative numbers. An 8-bit unsigned value would normally have a range of 0 to 255, but 127 is added to the exponent, giving it a range of -126 to +127.

Follow these steps to convert a number to FPS format.

1. First convert the number to binary.

2. Normalize the number so that there is one nonzero digit to the left of the binary place, adjusting the exponent as necessary.

3. The digits to the right of the binary point are then stored as the mantissa starting with the most significant bits of the mantissa field. Because all numbers are normalized, there is no need to store the leading 1.

   Note: Because the leading 1 is dropped, it is no longer proper to refer to the stored value as the mantissa. In IEEE terms, this mantissa minus its leading digit is called the significand.

4. Add 127 to the exponent and convert the resulting sum to binary for the stored exponent value. For double precision, add 1023 to the exponent. Be sure to include all 8 or 11 bits of the exponent.

5. The sign bit is a one for negative numbers and a zero for positive numbers.

6. Compilers often express FPS numbers in hexadecimal, so a quick conversion to hexadecimal might be desired.

IEEE FPS floating point formats

Here are some examples using single precision FPS.

3.5 = 11.1 (binary)
    = 1.11 x 2^1    sign = 0, significand = 1100...,
                    exponent = 1 + 127 = 128 = 10000000

    FPS number (3.5) = 0100000001100000...
                     = 0x40600000

100 = 1100100 (binary)
    = 1.100100 x 2^6    sign = 0, significand = 100100...,
                    exponent = 6 + 127 = 133 = 10000101

    FPS number (100) = 010000101100100...
                     = 0x42c80000

What decimal number is represented in FPS as 0xc2508000? Here we just reverse the steps.

0xc2508000 = 11000010010100001000000000000000 (binary)

sign = 1; exponent = 10000100; significand = 10100001000000000000000
exponent = 132 ==> 132 - 127 = 5

-1.10100001 x 2^5 = -110100.001 = -52.125

2.3.4. Byte Order

Big/Little Endian Memory Maps

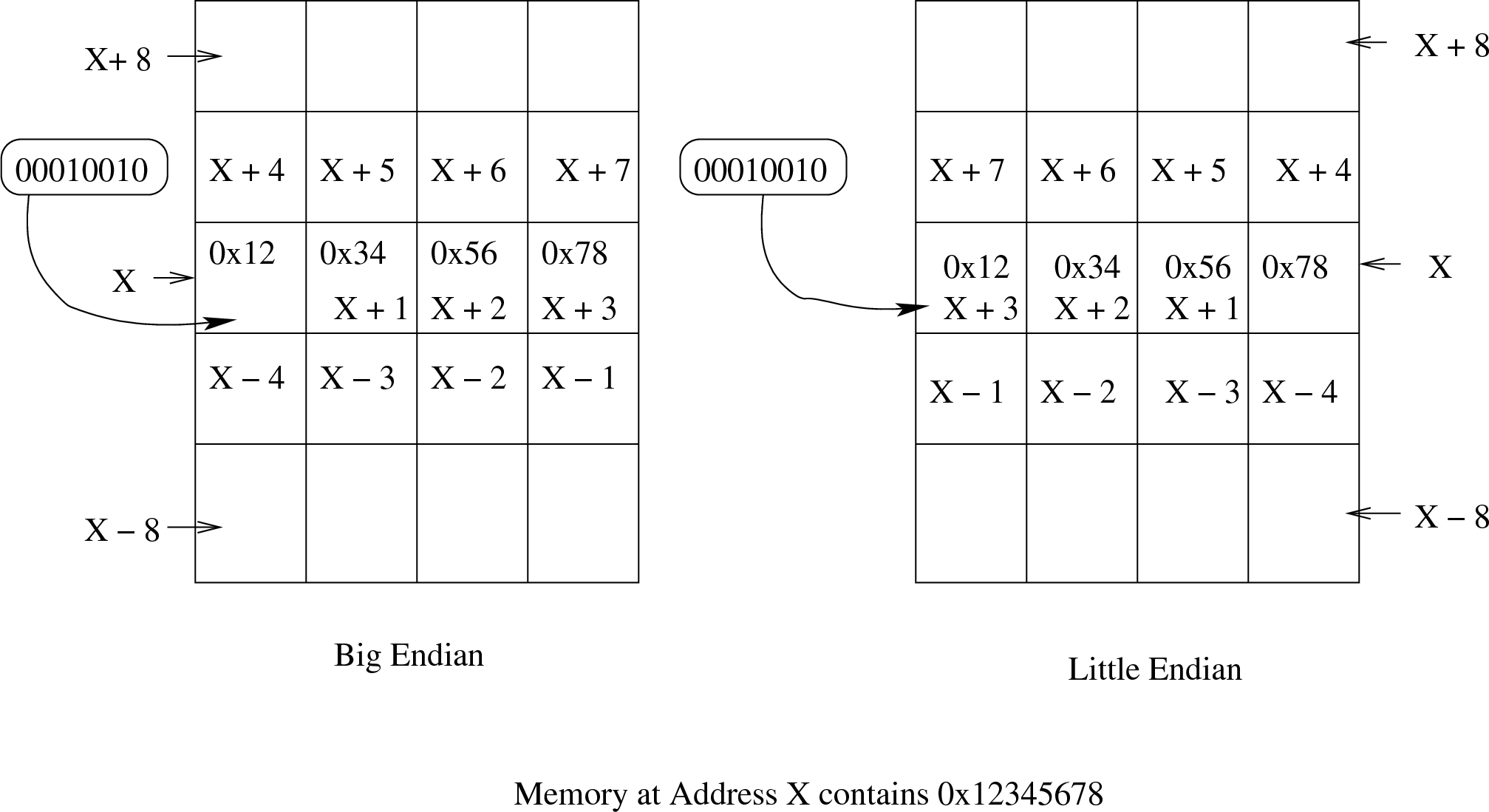
Not all computers store the bits (and bytes) of a variable in the same order. The Intel x86 line of processors stores the least significant bit in the lowest memory address (right most position) and the most significant bit in the highest memory address. This scheme is called Little Endian.

Sun SPARC and most other UNIX platforms do the opposite. They store the most significant byte in the lowest memory address. SPARC is thus considered a Big Endian machine. In a TCP/IP packet, the first transmitted data is the most significant byte, thus the Internet is considered Big Endian.

The lowest memory address is considered the memory address for a variable. Hence we see a difference between Little Endian and Big Endian when we draw memory maps. With Little Endian (Intel) we label the location of an address on the right side of the map. With Big Endian (SPARC), labels are placed on the left side of the map.

The term is used because of an analogy with the story Gulliver’s Travels, in which Jonathan Swift imagined a never-ending fight between the kingdoms of the Big-Endians and the Little-Endians, whose only difference is in where they crack open a hard-boiled egg.